東京女子学園　21世紀型授業（２）

東京女子学園では、キャリアガイダンス、ワールドスタディという大型プロジェクト型学習（ＰＢＬ）の学びの体験のエッセンスを教科の授業の中に埋め込めないかどうか議論が起こり、プロトタイプは何かリサーチが始まっている。

というよりも、すでに暗黙知として埋め込まれているので、それを可視化する議論になっている。そのＰＢＬの学びの体験が埋め込まれている数学の授業、小林俊道先生の高2の授業を拝見した。

「つり合う点を考える」という授業で、中学受験の理科のてこの問題のようなケースから始まっていた。三か所に個数の違うおもりをぶらさげて、どこでつり合うのかという問いが投げかけれれた。

実は前回の授業で、だいたいこのへんという感覚を、実際のてこを使って、実感するという感覚と体験を一致させる体験をし、そこから

全体の重り×つり合う点＝重り×目盛+重り×目盛+重り×目盛+・・・・・・

という一般化が行われていた。

前回の確認を、モデル化して生徒と共有する導入から始まっていたのである。プロジェクト型学習（ＰＢＬ）の構成要素に、“learning by making”という学びの体験がある。理科の実験などその一つであるし、社会のフィールドワークも典型例だろう。そしてこの学びの体験から、何らかの法則を見出すという一般化を行う。この「learning by making→一般化」という学びのプロセスは、20世紀型授業とは確かに違う。

従来は「一般化を教え込む→演習」という授業展開であり、学びのプロセスは軽視されてきた。これは演習問題の解き方の過程とは全く別次元のものである。21世紀型は、この一般化を導き出すのに、「体験」を媒介にする。実はこの「体験」の過程で、生徒は自らの内に疑問がわいてくる。新たな問いがでてくると、解決したくなる。モチベーションの内燃する場がそこには広がる。

しかし、数学でも実施しているとはやはり予想外だった。だが、たしかに、生徒は楽しそうに授業に参加しているし、真剣に取り組む。この楽しいから真剣になることを、ＰＢＬではフロー状態と呼ぶ。こうなってくると、その学びの体験は「プレイフルラーンニグ」と呼ばれるＰＢＬになる。小林先生の授業は、見事にＰＢＬのエッセンスが反映している。

ただし、ＰＢＬのエッセンスとは、学びのスタイルだけの話ではない。その学びの体験によって抽出された「一般化」の方法が肝なのである。ＰＢＬにおける「一般化」の方法は2つある。1つは言語記号論的手法。もう1つは数理的思考法である。国語や英語と数学の話？とすぐに思われるだろうが、これはメタ認知次元の話で、教科横断的次元の思考方法である。

国際バカロレアのＤＰではこの思考方法をトレーニングする教科があるし、それはイギリスのＡレベルでも米国のＡＰでもそうだ。またフランスのリセでは、高3で哲学が週に4時間あって、きっちりトレーニングされる。世界標準のＰＢＬのエッセンスである「ディスカッション」は、こうした言語記号論的手法や数理的思考法のトレーニングが前提である。

したがって、昨今双方向型の授業とかアクティブラーニングでディスカッションなどと言われているが、それらの多くが、このメタ認知次元のトレーニングを行わないままそれらしき体験をしているものが多く、小林先生のように数理的思考法を生徒と共有する東京女子学園のＰＢＬのエッセンスは、世界標準に到達しているといえるのではないか。では、どういうところが数理的思考法なのか。

それは、てこのリアルな体験を一般化する時に上記のように方程式に「置き換え」ているところに現れている。数理的思考法とは、どこまでもシンプルな方程式に「置き換える」操作である。この方程式に変換する体験をショートカットしてしまうのが20世紀型授業だった。小林先生はそこを生徒とシェアするチャンスを大切にしている。

ここで肝なのは、中学受験におけるてこの問題と目盛の取り方が違うという点である。てこの棒は、実は座標のｘ軸の見立て（メタファ）に過ぎない。このメタファという介在が、言語記号論的手法で、見事に数理的思考とコラボができている。

しかし、最終的には数理的思考は、言語記号論的手法を必要としない座標系の世界に突入する。ＩＢのＤＰのハイレベルマスでは、この領域をデンジャラスナレッジと呼んで、数学が好きな生徒が取り組む世界だそうだ。

ともあれ、小林先生のつり合いを求める基礎は、ｘ軸上のものであったのだから、当然ながら発展的な学習には、いよいよy軸が登場してくれる。そこで、次のように正方形の4分の１をカットし、カットした正方形を別の4分の１のエリアに貼り付けて、コマをつくるとしたら、つり合う点はどこになるかという新たな問いに発展する。

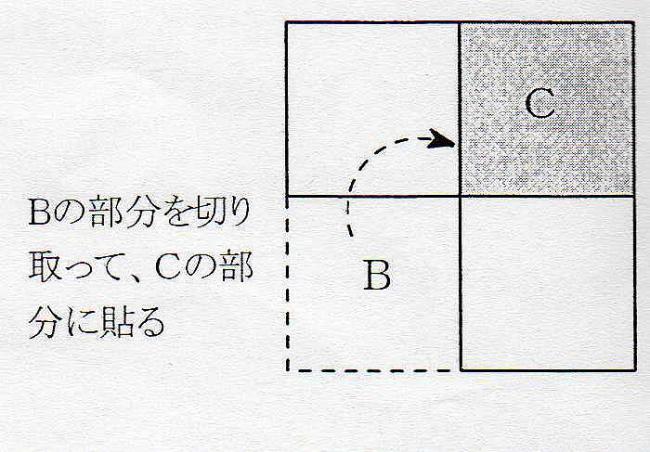
この段階では、実際にコマをつくりながら、つり合う点を探し当てる“learning by making”が行われる。

コマをつくる過程で、今度はx軸上で一般化した方程式を「適用」して、点を求める数理的思考も組み立てる。

しかし、ここにまた大きな壁が現れる仕掛けになっている。というのは、切り取った4分の1カット分の重さをどう考えるかだ。言語的には、1は１でしょうとなる。最初多くの生徒はそこに疑いを持たない。しかし、小林先生が、カットした分を貼りり付けたわけだから、総量は４であるのは変わらないはずというと、生徒はまさか－１・・・と応える。

授業終了後に、小林先生は、空集合や方程式の計算過程でA/A=1を掛け合わせるとか、補助線とか、ないものを０ととらえるか－１ととらえるかは、重要な数学的発想だと言われた。また、コマの学びの体験は、ベクトルや行列の導入でもあると。

結局、数理的思考法の肝は、いかに関数を創り出せるかというところにあったのだ。そしてこれがＰＢＬの最も重要なエッセンスである。

生徒たちは、小林先生のめざす数理的思考法を、実際にコマを回し、検証しつつ身につけていっているのだろう。中にうまく回らない生徒がいたが、小林先生はニコニコしながら、その生徒に数理的思考法を確認するチャンスを与えてくれてありがとうと語りかけるかのように、コマが回る回らないという現象は何を意味するのかと問いかけた。